راهنمای نگارش ریاضی به انگلیسی

دکتر کوین پی لی
اینجا کلاس ریاضی است! پس چرا از نگارش میگوییم؟
به احتمال زیاد تاکنون در کلاس ریاضی مقالهای ننوشتهاید؛ بنابراین ممکن است الان تعجب کنید که چرا باید در کلاس ریاضی به مبحث نگارش بپردازیم.
کلمهٔ یونانی mathemas، که کلمه ریاضیات از آن گرفته میشود، دربرگیرندهٔ مفهوم دانش، شناخت، فهم و ادراک است. درنهایت میتوان گفت که ریاضیات در مورد ایدهها است. در کلاسهای ریاضی سطح دانشگاهی، ایدهها و مفاهیم ارائهشده پیچیدهتر و در سطوح بالاتر هستند. ریاضیاتی که در دانشگاه تدریس میشود شامل مفاهیمی است که صرفاً با معادلات و فرمولها نمیتوان آنها را بیان کرد. نگارش مقالهٔ ریاضی علاوه بر معادلات و فرمولها نیازمند نوشتن جملات و پاراگرافها نیز هست.
در حقیقت، نگارش ریاضیات بسیار زمانبر است. اگر ریاضیدانان بخواهند به گسترش پیکرهٔ دانش ریاضیات کمک کنند، باید بتوانند ایدههای خود را به روشی قابلفهم به دیگران ارائه کنند. بنابراین، توانایی نگارش واضح ریاضیات مهارتی است که بهاندازهٔ توانایی حل معادلات ریاضی مهم است. تبحر در نوشتن توضیحات ریاضی، بهشکلی واضح، برای افراد غیر ریاضیدان نیز مهم است. اگر بهطور پیوسته در کلاسهای ریاضی دانشگاه شرکت کنید، دانش ریاضی شما بیشتر از سایر افراد خواهد شد. زمانی که از دانش ریاضی خود در آینده استفاده کنید، ممکن است لازم باشد تا فرایند فکری خود را به دیگران (مثلاً رئیستان، همکار یا یک مقام منتخب) توضیح دهید و این احتمال وجود دارد که دانش ریاضی این فرد از شما کمتر باشد. اگر یاد بگیرید که چطور ایدههای ریاضی را بهطور شفاف به دیگران ارائه دهید، در حرفهٔ خود پیشرفت خواهید کرد.
پس متوجه میشوید که نگارش خوب توضیحات ریاضی موجب ارتقای دانش و درک شما از ایدههای ریاضی، که با آن سروکار دارید، میشود. به روی کاغذ آوردن ایدهها نیازمند توجه و تفکر دقیق است. ازاینرو، ریاضیاتی که بهطور شفاف و دقیق مکتوب شوند، احتمال صحیح بودنش بیشتر است. فرایند نگارش به شما کمک میکند تا مفاهیمی را که در کلاس ریاضی به آن پرداخته میشود، یاد بگیرید و حفظ کنید.
دانلود چک لیست نگارش ریاضی برای رعایت تمام نکاتی که در این مقاله به آن اشاره شده است.
نگارش صحیح ریاضیات چگونه است؟
هرچه بیشتر ریاضیات را یاد بگیرید، توانایی بیان ایدههای ریاضی اهمیت بیشتری پیدا میکند. طولی نمیکشد که دیگر نوشتن «پاسخ» نهایی کفایت نمیکند. هرمن ملویل دلایل قابلقبولی دارد که «موبی دیک» را در قالب یک رمان نوشته است و فقط به این تکجمله که «نهنگ بحر برنده میشود» اکتفا نمیکند.
دقیقاً به همین دلیل است که در کلاسهای ریاضی دانشگاه فقط نوشتن نتیجه نهایی مسئله کافی نیست.
نگارش ریاضیات را نباید با «نمایش کارتان» اشتباه بگیرید. نگارش مقالهٔ ریاضی نباید به این هدف انجام شود که نشان دهد شما تکلیفتان را انجام دادهاید؛ بلکه هدف این است که نشان دهید مفاهیم و ایدههای ریاضی را بهخوبی درک کردهاید. لیستی از محاسبات، بدون هیچگونه متن یا توضیح بیانگر آن است که زمانی را صرف محاسبات کردهاید؛ هرچند، لیستی از محاسبات فاقد توضیح معادل حذف ایدههاست. ایدهها یعنی ریاضیات. بنابراین، صفحهای پر از محاسبات فاقد متن یا توضیح یعنی هیچ ریاضیاتی در آن وجود ندارد.
زمانی که مقالهایی را در کلاس ریاضی مینویسید، هدف شما انتقال شفاف ایدهها و استدلالهای ریاضی به افراد دیگر است. نگارش انجامشده در کلاس ریاضی بسیار شبیه نگارش در سایر کلاسهاست. احتمالاً قبلاً عادت داشتهاید برای دروسی نظیر روانشناسی، تاریخ و ادبیات مقاله بنویسید. میتوانید بسیاری از دستورالعملهایی را که هنگام نگارش مقاله در خصوص دروس دیگر باید رعایت کنید، در نوشتن مقالهٔ ریاضی نیز رعایت کنید.
در صورتیکه به بحث نگارش فنی و علمی علاقه دارید، پیشنهاد میکنیم مطالب زیر را هم مطالعه کنید:
اصول ابتدایی: ترکیب واژگان و معادلات
پیروی از قواعد دستوری
در نگارش خوب قواعد دستوری رعایت میشود. این قاعده در نگارش مقالات ریاضی نیز صدق میکند! زمانی که مقالهای را در کلاس ریاضی مینویسید، انتظار میرود که املا و قواعد دستوری آن صحیح باشد. نگارش شما باید شفاف و حرفهای باشد. از آوردن اختصارها یا مخففهایی که مطابق با قواعد استاندارد نگارش نیستند، پرهیز کنید. ریاضیات را با نوشتن جملات و ایجاد پاراگرافها مکتوب میکنیم. (بله درست است، پاراگرافها مهم هستند. خواندن مقالهای سهصفحهای متشکل از فقط یک پاراگراف اصلاً جالب نیست.)
البته یک مورد هم وجود دارد که صرفاً به نگارش ریاضی مربوط میشود و در سایر نگارشها یافت نمیشود: فرمولها. ممکن است تعجب کنید اگر بفهمید که در نوشتههای ریاضی، فرمولها و معادلات نیز از قوانین دستوری استاندارد حاکم بر کلمات پیروی میکنند. نمادهای ریاضی میتوانند معادل عبارات گفتاری مختلف باشند. بهعنوانمثال، جملهٔ زیر، کامل و کاملاً صحیح نوشته شده است.
2=1+1
نماد «=» مانند فعل عمل میکند. جملات کامل دیگری در زیر آورده شده است.
آیا میتوانید فعلها را مشخص کنید؟ از سوی دیگر، عبارتی مانند:
جملهٔ کامل محسوب نمیشود؛ زیرا هیچ فعلی ندارد. چنین عبارتی را باید عبارت اسمی در نظر گرفت. آیا میتوانید اسمها را در مثالهای قبل مشخص کنید؟
فرمولها و معادلات باید در جملات کامل و با نشانهگذاری صحیح آورده شوند. به مثال زیر توجه کنید:
The total revenue, R, made from selling widgets is given by the equation
where p is the price at which each widget is sold and q is the number of widgets sold. Based on past experience, we know that when widgets are priced at $15 each, 2000 widgets will be sold. We also know that for every dollar increase in price, 150 fewer widgets are sold. Hence, if the price is increased by x dollars, then the revenue is
به نشانهگذاری انتهای معادلات دقت کنید. محاسبهای که در آن جمله به پایان میرسد، نیاز به نقطه دارد. محاسباتی که در آن جمله تمام نمیشود، نیاز به ویرگول دارد.
روش مناسبی که برای بهبود نگارش ریاضی وجود دارد آن است که نوشتهٔ خود را به انضمام تمام معادلات با صدای بلند بخوانید. گوشهای شما بهتر از چشمانتان میتوانند خطاهای دستوری و جملات ناقص دستوری را تشخیص دهند. اگر متوجه شدید که یک سری معادله و جملات ناقص را میخوانید، باید نوشتۀ خود را بازنویسی کنید.
نکات مهم دیگری نیز در مثالهای بالا به چشم میخورند. به نحوهٔ نگارش کلمهٔ «we» دقت کنید. استفاده از اول شخص در ریاضیات امری رایج است، بهویژه اول شخص جمع «we»، بنابراین نگران نوشتن این کلمه در مقالات کلاس ریاضی خود نباشید.
نکتهٔ مهم دیگر این است که معادلات مهم یا طولانی در خطهای جداگانه نوشته میشوند. اگر هر معادله مهم را در یک خط جداگانه بنویسید، مقالۀ شما راحتتر خوانده میشود. جدا کردن فرمولهای مهم در متن زیر کار دشواری است:
If d is Bob’s distance above the ground in feet, then d=100-16t2, where t is the number of seconds after Bob’s Flugelputz-Levitator is activated. Solving for t in the equation d=100-16t2, we find that t=2.5. Bob hits the ground after 2.5 seconds.
اگر متن فوق را بهصورت زیر بنویسیم واضحتر است:
If d is Bob’s distance above the ground in feet, then
where t is the number of seconds after Bob’s Flugelputz-Levitator is activated. Solving for t in the equation
we find that t=2.5. Bob hits the ground after 2.5 seconds.
نمادها و واژگان
استفاده صحیح از نمادها و واژگان اهمیت بالایی دارد. یکی از مواردی که به نگارش بهتر ریاضیات کمک میکند آن است که بدانیم چه موقع از از نمادها و چه موقع از واژگان استفاده کنیم.
وقتی منظورتان دقیقاً چیز دیگری است، از نمادهای ریاضی استفاده نکنید. یکی از اشتباهات رایج، استفادهٔ نادرست از نماد «=» است. بهعنوانمثال:
زمانی که منظورتان این است که «گام بعدی این است که» یا «بهعبارت دیگر، یعنی» از علامت مساوی استفاده نکنید. مثال بالا واقعاً میگوید 1 = 0 = 1- استفاده از علامت پیکان بهجای مساوی اندکی بهتر است اما باز هم مناسب نیست:
وقتی با یک سری از محاسبات مواجه هستیم، گاهی بهتر است هر معادله را در خطی جداگانه بنویسیم.
برای محاسبات مشکل که خواننده ممکن است نتواند بهراحتی مراحل را دنبال کند، میتوانید برای توصیف هر مرحله، از کلمات نیز استفاده کنید.
البته، حواستان باشد که برگهتان یک ستونه باشد. هیچ محاسبهای را «بهصورت دوستونه» توضیح ندهید.
خواندن این محاسبه سخت است. سبک نگارشی آن نیز بد است.
بعضی چیزها را با کلمات بهتر میتوان توضیح داد؛ اما برخی دیگر با نمادهای ریاضی بهتر بیان میشوند. برای مثال، خواندن جملات زیر سخت است:
It follows that x plus two is larger than zero.
در اینجا، استفاده از نماد ریاضی بسیار مناسبتر است.
It follows that x + 2 > 0.
نکات متفرقه
در ادامه مثالهای دیگری ارائه شده است تا شما را در شروع نگارش ریاضیات کمک کند.
- هیچ جملهای را با فرمول آغاز نکنید. اگرچه از لحاظ دستوری صحیح است، اما ملموس نیست.
t = 5 when w = 2000, so we can conclude that the new factory will be completely overrun with cockroaches in 5 years.
f is globberuxible at x = 3.
افزودن تنها یک یا دو کلمه میتواند این مثالها را تصحیح کند.
Since t = 5 when w = 2000, we can conclude that the new factory will be completely overrun with cockroaches in 5 years.
The function is globberuxible at x = 3.
- نوشتههای بدخط و ناخوانا را به استاد خود تحویل ندهید. در دانشکده، مقالات باید تایپ شوند و معمولاً یک خط در میان و با حاشیههای زیاد نوشته شوند. مقالات ریاضی از همان استاندارد مقالات سایر کلاسها پیروی میکنند.
- اگرچه تایپ کردن مقاله ایدهٔ خوبی است، ممکن است مجبور شوید جای فرمولها را خالی بگذارید و بعداً آنها را دستی بنویسید. دستی نوشتن فرمولهای مقالات ریاضی کاملاً قابلقبول است. فقط مراقب باشید نمادهای ریاضیتان خوانا باشند. اگر تصمیم دارید معادلات را تایپ کنید، فراموش نکنید که متغیرهای معادلات و فرمولها معمولاً بهصورت کج نوشته میشوند (تا در متن متمایز باشند). بسیاری از برنامههای پردازش کلمات دارای ابزار ویرایشگر معادله هستند. در نسخههای جدیدتر برنامهٔ Microsoft word، ابزار ویرایشگر معادله زیر منوی Insert قرار دارد. گزینهٔ .. و سپس Equation را انتخاب کنید. اگر قصد دارید متون فنی زیادی را تایپ کنید، بهتر است کار با دو زبان حروفچینی حرفهای ریاضی، TEX یا LATEX را یاد بگیرید. این متن با LATEX نوشته شده است. همچنین ممکن است تایپ مقالات در برنامهٔ Maple یا سایر نرمافزارهای مخصوص ریاضی نیز برایتان رضایتبخش باشد.
- از نمادهای ریاضی بهدرستی استفاده کنید. وقتی نوشتن معادلات پیچیدهتر ریاضی را فرامیگیرید، جا افتادن نمادها از فرمولها بسیار ساده میشود. استفادهٔ صحیح از نمادها را فرابگیرید!
- زبان نوشتاری را دقیق و صحیح استفاده کنید. مراقب باشید کلماتی که استفاده میکنید دقیقاً همان معنای موردنظر شما را منتقل کنند. ریاضیات نیازمند استفاده بسیار دقیق از زبان است. مورد دیگری که باید از آن اجتناب کنید، استفادهٔ بیشازحد از ضمیر “it” است. خواندن مقالات ریاضی که پر از ضمیرهای «it» و «that» است معمولاً کار دشواری است. خواننده اغلب بهسختی متوجه میشود که ضمیر «it» به چه چیزی اشاره میکند. اگر شمای نویسنده نیز در پیداکردن مرجع «it» مشکل دارید، ممکن است با ایدههای ریاضی مشکل داشته باشید. ممکن است لازم باشد قدری بیشتر دربارۀ موضوعی که دارید مینویسید، فکر کنید.
- سعی کنید تا حد امکان ساده و مستقیم بنویسید. هیچکس دوست ندارد نثرهای سنگین و متکلف را بخواند.
ایدههای ریاضی در نوشتار
مرتب کردن مقاله
خواندن مقالهٔ مرتب راحتتر از مقالهٔ بههمریخته است. خوشبختانه، چندین روش استاندارد برای نظمبخشی به مقالات ریاضی وجود دارد.
ابتدا، چند نوع مقدمه وجود دارد. معمولاً مسئله اصلی در مقدمه بیان میشود. حتی اگر به مسئلهای از کتاب درسی هم پاسخ میدهید، نباید فرض کنید که خواننده با کتاب درسی آشنایی دارد یا حتی یک نسخه از آن کتاب را پیش خود دارد. البته شما نیز مسئله را صرفاً رونویسی نکنید! بلکه سعی کنید مسئله را به زبان خود بازنویسی کنید.
مقدمهٔ خوب باید دربارۀ اهمیت مسئله نیز توضیح دهد. در قسمت مقدمه باید بتوانید خواننده را اصطلاحاً به «قلاب» بکشید.
بد نیست در مقدمه از سایر قسمتهای مقاله نیز بهاختصار نام ببرید. شِمایی از محتویات مقاله را در قسمت مقدمه به خواننده ارائه دهید.
We will analyze the revenue using a linear model and then examining the graphs generated by the model.
The production of fava beans will be modeled using a C program.
First, we will analyze the population using numerical methods. Then, we will analyze the population using formulas. We will then compare the two different results.
در برخی مقالات، «پاسخ» به مسئله بلافاصله پس از مقدمه آورده میشود. برخی مقالات نیز «پاسخ» را در انتهای مقاله میآورند. این کار سلیقهای است. گاهی اوقات، نتیجهٔ نهایی مهمترین چیز در مقاله است. ممکن است لازم باشد برای جلب توجه خواننده، نتیجهٔ نهایی را در همان ابتدای مقاله بیان کنید. از طرف دیگر، گاهی اوقات شیوهٔ رسیدن به نتیجه نهایی مهمتر است. در چنین موردی، بیان نتیجهٔ نهایی در پایان مقاله ممکن است عاقلانهتر باشد.
درهرصورت، بهتر است با استفاده از اصطلاحهای دنیای واقعی، نتیجهٔ مسئلهٔ اصلی را بیان کنید.
The solution is t = 6.
The solution to the equation is t = 6. The population of Utopia is at its smallest 6 years after the plague begins
دقت کنید استدلالهایی را که مینویسید با دقت سازماندهی شده باشند. بهتر است قبل از نوشتن مقاله ریاضی، طرح کلی آن را بنویسید. نوشتن طرح کلی به شما کمک میکند تا واضحتر به مفاهیم فکر کنید و بالتبع مطالب را بهتر یاد بگیرید. مادامیکه در مورد مسائل پیشرفتهتر ریاضی مینویسید، سازماندهی مطالب اهمیت بیشتری پیدا میکند.
در سطح مخاطب خود بنویسید
برای اکثر مقالاتی که در کلاس ریاضی مینویسید، باید فرض کنید که دانش ریاضی خواننده در حد شماست. وقتی راهحل مسئلهای را که از تکالیف درسی دانشآموزان است، مینویسید، بهتر است فکر کنید که برای دانشآموزی در بخش دیگری از کلاس یا برای کلاسی مشابه در مدرسهای دیگر مینویسید. برخی مقالاتی را که مینویسید، به خوانندهای ارائه میشود که دانش ریاضی کمتری نسبت به شما دارد. هدف از نگارش مقاله ریاضی این نیست که به استاد نشان دهید مطلبی را میدانید، زیرا استاد شما از آن مطلب آگاه است. شما مقاله را برای او نمینویسید، بلکه برای کسی مینویسید که مطلب را نمیداند. (آن شخص میتواند خود شما باشد! میتوانید از این تکلیف خود (نگارش مقاله) برای مرور مطالب بهمنظور آمادگی برای امتحان استفاده کنید.)
در نگارش ریاضیات، دلیل و نحوهٔ رسیدن به راهحل را برای خواننده توضیح میدهید. همچنین ممکن است بخواهید خواننده را متقاعد کنید که استدلال و روش خاص شما در رسیدن به راهحل موردنظر صحیح است. مقالهٔ ریاضی خوب نهتنها باید توضیحات شفافی را ارائه دهد، بلکه باید بتواند خوانندهٔ مردّد را نیز مجاب کند.
بسیاری از اوقات، اگر بتوانید از مسیرهای مختلف به یک راهحل برسید، میتوانید مقالهٔ خود را متقاعدکنندهتر کنید. ممکن است بخواهید مسئلهای را هم با استفاده از کامپیوتر و هم بهصورت جبری آنالیز کنید؛ یا گرافی را با اطلاعات دنیای واقعی مقایسه کنید. تصاویر و طرحهای گرافیکی میتوانند برای خواننده بسیار مفید باشند.
مثالهای خاص نیز به متقاعدکنندهتر کردن نوشته شما کمک میکنند. برای اینکه به خواننده کمک کنید تا استدلال انتزاعی کلی را بهتر درک کند، میتوانید چگونگی صدق کردن آن استدلال را در موردی خاص نشان دهید. همچنین میتوانید از موارد «کرانی یا همان اکسترممها» برای نشان دادن محدودیت استدلال استفاده کنید.
در هر لحظهای که نیاز به خدمات ترجمه تخصصی داشتید میتوانید سفارش آنلاین خود را در شبکه مترجمین ایران ثبت کنید.
مراقب باشید هرچه مینویسید به مسئله ربط داشته باشد. گنجاندن اطلاعات و توضیحات بیشازحد نشاندهندهٔ عدم درک شما از ایدهها و مفاهیم است و درنتیجه اثربخشی کلی نوشته ریاضیتان را کاهش میدهد. با فکر کردن به خواننده میتوانید تصمیم بگیرید که چه جزئیاتی را در مقاله بگنجانید و از چه جزئیاتی صرفنظر کنید. محاسباتی را که برای خواننده خستهکننده و ملالآور باشند، میتوانید بهراحتی حذف کنید. (باز یادآور میشویم که نوشته ریاضی برای نشان دادن تکلیف کاری نیست. لازم نیست همه چیز را نشان دهید.) خوانندهٔ یک مقاله ریاضی دانشگاهی قطعاً تمایلی به خواندن چگونگی ضرب 5 در 74 ندارد. موارد غیر مهم را حذف کنید. از سوی دیگر، تمام چیزهایی را که برای توضیح ایدههای مهم مقالهٔ شما ضروری هستند، بیاورید. یادگیری موارد مهم و غیر مهم به شما کمک میکند تا ریاضی را بهتر درک کنید.
نباید فرض کنید خواننده با مسئلهای که میخواهید حل کنید آشنا است. درحالیکه نیازی نیست مسئله را بهطور کامل بازگو کنید، نباید از بیان تمام جزئیات مهم در مسئله نیز غافل شوید. همچنین نباید طرز فکر خواننده را شبیه طرز فکر خود فرض کنید. در نوشتهتان، تمام فرضیات خود را بیان کنید. بهعنوانمثال، در مسائل فیزیک، اغلب فرض میشود که تمام اشیاء فاقد اصطکاک هستند. اما بیان تقریباً همیشگی این فرضیه دلیل نمیشود که خواننده نیز بهطور خودکار این فرضیه را در ذهن خود تصور کند. خواننده ممکن است با فیزیک آشنا نباشد. اینکه شما چیزی را درست میپندارید، به این معنا نیست که خواننده نیز آن را درست میپندارد. پس آن را بنویسید.
تعریف متغیرها و فرمولها
کمیتها و توابع را میتوان با حروف نیز نشان داد و اغلب نیز باید چنین کرد. البته، حروفی که انتخاب میشوند اختیاری هستند. باید بهطور صریح و با دقت هر چه تمام، حروف بهکار رفته در فرمولها را توضیح دهید. بهعنوانمثال:
Either n or n + 1 is even
n چیست؟ اگر n=8.5 باشد، آیا عبارت بالا درست است؟ روش بهتر برای بیان این عبارت به این صورت است:
For any whole number n, either n or n + 1 is even.
یکی از عبارات رایج در ریاضیات “Let…” است.
Let x be any real number.
Let P be the population of Los Angeles in 2010.
Let f(x) = x2+1.
در مثال آخر، x یک جایبان است و نیاز چندانی به معرفی ندارد؛ اما بهتر است بنویسیم:
Let f(x) = x2 + 1 for all real numbers x.
اگر توصیف تمام متغیرها خستهکننده میشود، سعی کنید هیچ متغیری را توضیح ندهید. بدیهی است که مثال زیر نیاز به اصلاح دارد.
مثال زیر کافی ولی طولانی است.
مثال بالا را میتوانیم با حذف متغیرها زیباتر کنیم.
The volume of the box is the product of the length, the width, and the height.
در تعریف متغیرهایی که بیانکنندهٔ کمیتهای دنیای واقعی هستند باید محتاطتر عمل کنید. سعی نکنید آنها را مبهم توصیف کنید، مانند مثال زیر:
Let D(t) be the distance at a time t.
گنجاندن واحدها میتواند مثال بالا را واضحتر کند اما ابهام توصیف همچنان باقی است.
Let D(t) be the distance in miles at t hours.
سعی کنید تا حد امکان دقیق باشید.
Let D(t) be Agnes’s distance from the arena in miles t hours after the riot began.
همچنین، دقت کنید که هر نمادی که استفاده میکنید، تنها بیانگر یکچیز باشد. این مسئله حساستر از آن چیزی است که به نظر میرسد. مثال زیر ظاهراً واضح است.
Let P be the escaped wombat population (in thousands) t years after 1990 and suppose that
The wombat population in 1992 is approximately 672. We can see this by setting t = 2 and observing that
If we want to predict when the wombat population will reach 2000, we set P = 2 and solve for t using logarithms.
The wombat population will reach 2000 in the year 2002.
فکر میکنم هیچ خوانندهای نتواند به مثال بالا ایراد بگیرد، زیرا ظاهراً واضح و قابلفهم است. متغیر P همیشه برای اشاره به جمعیت وامبتها استفاده میشود. البته دقت کنید که در پاراگراف اول، P به جمعیت وامبتها بهطورکلی اشاره دارد. در پاراگراف بعد، P =0.6272، به جمعیت وامبتها در سال 1992 اشاره دارد. در پاراگراف آخر نیز، P=2 است. به نظر میآید معنای P در هر بار استفاده تغییر میکند. در پاراگراف اول، P بیانگر جمعیت وامبتها در تمام زمانهاست. در قسمت بعد، P بیانگر جمعیت در زمانی خاص است. این مشکل را میتوان با حذف برخی متغیرها و افزودن متغیرهای دیگر رفع کرد.
Let P be the escaped wombat population (in thousands) t years after 1990 and suppose that
By substituting 2 for t in the above equation, we can see that in 1992, the wombat population is approximately 672.
Let t2000 be the year when the wombat population reaches 2000. Then,
The wombat population will reach 2000 in the year 2002.
در مثال بالا، میتوانیم با متغیرها اندکی تغییر ایجاد کنیم اما این کار در مسائل پیچیدهتر میتواند منبع مشکلات بالقوه باشد. وقتی از یک نماد برای نشان دادن دو چیز متفاوت استفاده میشود (حتی، یا اگر بهطور خاص، آن دو چیز مشابه نیز باشند)، خواننده (و خود نویسنده!) ممکن است سردرگم شود. نمادی که به دو شیوه مختلف استفاده شود نهتنها گیجکننده است، بلکه اغلب به ریاضیات نادرست نیز منتهی میشود!
همانطور که متغیرها را باید با دقت معرفی کنید، در مورد فرمولها نیز باید مراقب باشید که آنها را شانسی استفاده نکنید. به خواننده بگویید که چگونه هر فرمول را به دست میآورید یا هر فرمول به چه معنی است. برخورد با فرمولها بدون هیچگونه هشداری اصلاً خوشایند نیست.
استفاده از تصویر در ریاضیات
گاهی یک تصویر از هزاران کلمه گویاتر است. بهشدت توصیه میکنم که در نوشتار ریاضیات خود از آرگومانهای تصویری نیز استفاده کنید. البته، اگر در نگارش خود تصویر، نمودار، گراف یا سایر مثالهای تصویری ریاضی را میگنجانید، حتماً نحوهٔ ارتباط آن با استدلال ریاضی خود را بهطور کامل توضیح دهید.
Looking at the graph, we can see that the result is true.
خواننده چه چیزی را باید در گراف مشاهده کند؟ دلیل پشتیبانی گراف از استدلال شما چیست؟ دقیقتر باشید.
The graph increases sharply at t = 3, confirming our earlier prediction that the robots will begin a homicidal rampage three years from now.
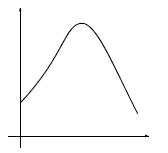
گراف خوب باید اطلاعات مرتبط و خاصی را به خواننده انتقال دهد. گراف زیر مبهم است.
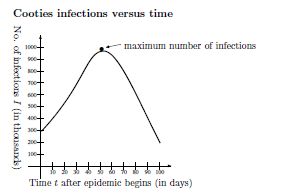
گرافها و نمودارها باید تمیز ترسیم شوند و بهدرستی برچسب بخورند. مقیاسهای روی محورها را نشان دهید. ویژگیهای قابلتوجه گرافیکی را مشخص کنید.
اگر میخواهید گراف را دستی رسم کنید، از خطکش استفاده کنید. میتوانید گراف را با استفاده از کامپیوتر نیز ترسیم کنید. درهرحال مراقب باشید. برنامههایی مثل Excel یا Microsoft Office معمولاً برای ترسیم گرافهای ریاضی مناسب نیستند. اگر از برنامههای ریاضی نظیر Maple استفاده کنید، موفقتر خواهید بود.
هر نموداری را که ترسیم میکنید باید با دقت برچسبگذاری نیز بکنید. حواستان باشد تا تمام مواردی را که در استدلالتان به آن اشاره کردهاید، برچسب بزنید.
سخن آخر
نگارش ریاضیات کار چندان سادهای نیست، مهارتی است که یادگیری آن نیاز به تمرین و تجربه دارد. منابع بسیاری در دانشگاه پوردو کالومت وجود دارند که میتوانند در نگارش ریاضیات به شما کمک کنند. Math Lab و Writing Lab نیز در میان این منابع وجود دارند.
اگر قبلاً مقالهٔ ریاضی زیاد ننوشتهاید، ممکن است در ابتدا ناامید شوید؛ اما یادگیری نگارش ریاضیات صرفاً با انجام آن محقق میشود. ممکن است در ابتدا سخت باشد اما با گذشت زمان سادهتر میشود و شما نیز در آن پیشرفت میکنید. ناامید نشوید! توانایی نگارش ریاضیات مهارت خوبی برای یادگیری است که تا آخر عمر برایتان میماند.

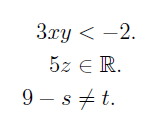
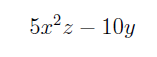
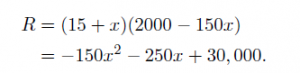
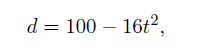
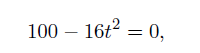
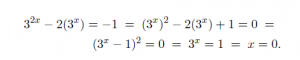
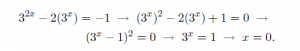
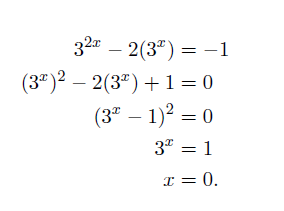
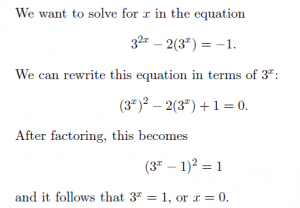

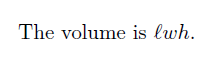
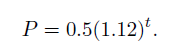
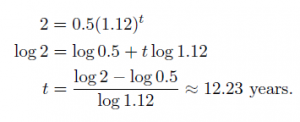
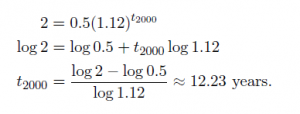



كامل نيست من علامت \dfrac و علامت * را در رياضي مى خواستم كه كوچكترين اشاره اي نشد لطفا مقاله را كسي بنويسد كه رياضي بداند در سايت quora لطفا مطالعه بيشتري كنيد
این مثاله ترجمه شده ی یک مقاله انگلیسی ست که این سایت زحمت ترجمه و نوشتاره روان و زیبای آن را کشیده اند
سلام خدمت تک تک عزیزان. اولا هیچ نوشته ای کامل نیست، حتی اگر ده هزار صفحه باشد. با این حال، نوشته ی بالا یک نوشته ی بسیار خوب و به درد بخور بود، کسانی که دنبال نمادهای جمع و ضرب و ستاره هستند، باید به موضوعات سطح پایینتر رجوع کنند. چون در اینجا به موضوعاتی پرداخته شده که سطح بالاتری دارند.